In the previous articles in this series, eight Large Language Models (LLMs) competed in a game of Categories (open source repo available here) to rank their capacity for producing distinct outputs. Then, increasing amounts of game information were provided to the AI players — both about their own prior responses, and the entire group’s previous choices.
Some models, like GPT-4o, remained relatively consistent and rigid in its output, even as more information was available. Other models, particularly the Anthropic Claude series of models, showed rapid adaptations to open information situations, both producing more distinct outputs, as well as discovering reward-hacking strategies to inflate their scores.
What we’ve seen so far is that models can be nudged out of obvious attractor basins to explore their their output space with only a simple one-turn feedback loop showing the model its own prior reasoning. One might notice that this information flow is exactly the same as the information flow within a Recurrent Neural Network (RNN) cell, but at a higher layer of abstraction, with the LLM taking the place of the RNN cell:
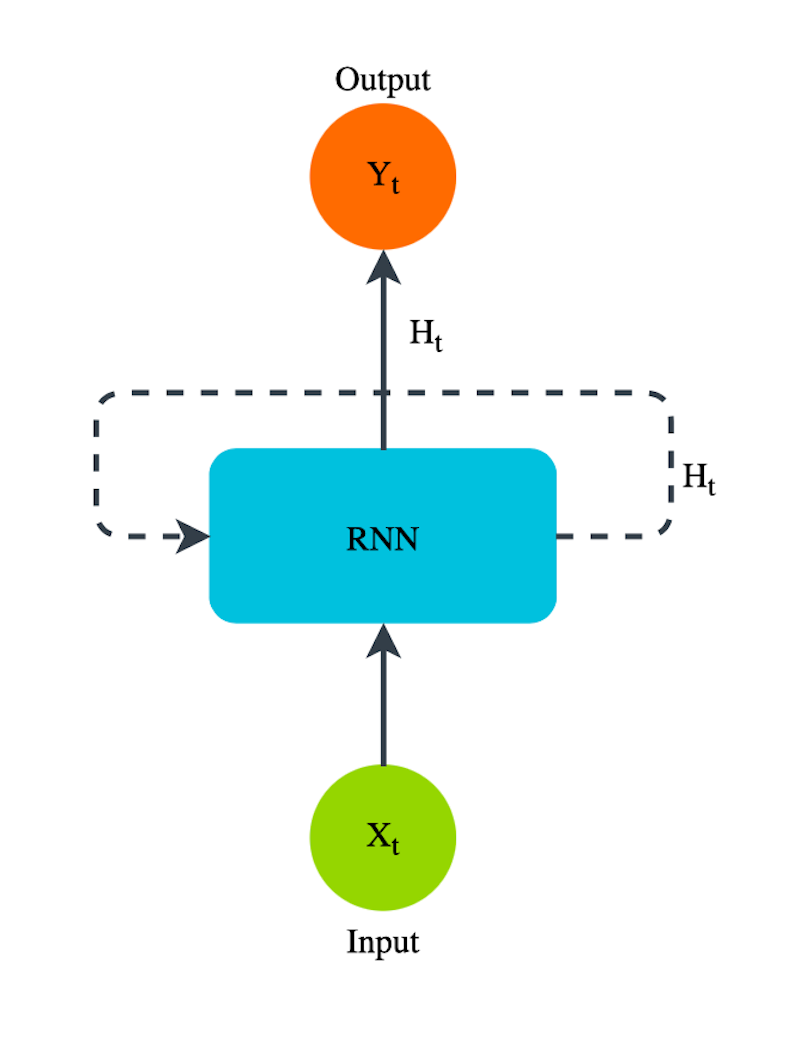
The Problem So Far
A shortfall of the tests conducted so far is that the results are conditioned on the specific group of models being compared and the specific number of players in the game. That means that any observations from this particular game configuration can’t be compared with observations with any other game condition. If, for example, we wish to test one or more additional models, we would either have to change the number of players or replace players in the game.
Either of those changes will make the scores incomparable between game conditions. If we wanted to rank the new model(s) relative to the old ones, an entirely new game condition would have to be run with all models participating. This means that obtaining this information. This means that if we wanted to maintain rankings for hundreds of models, hundreds of models would have to be competed against each other every time a new model appeared. Furthermore, scores would approach zero as number of players increased. Or else the data would be a constantly moving target as older models were discarded and newer ones included.
A Universal Comparison - Self-Play!
What’s needed is a context-independent score that can be obtained for any model individually and compared directly to other models tested at other times. Fortunately, the game of AI Categories provides an elegant solution—self-play!
As I pointed out in part 1 of this series, a useful property of AI Categories is that it’s simultaneously competitive and cooperative. That is, players can achieve different scores that can be used to rank them, but within the game, players have no incentive to prevent other players from scoring points, nor any ability to do so without sacrificing at least an equivalent number of points themselves. This is a consequence of the “unique response” scoring mechanism. A maximally informed player is incentivized to avoid duplication with other players, making it more likely that those other players score points as well. Consequently, games played among many high-skilled players should show high total scores as well as high individual scores.
In a 2-handed play condition, the competitive dimension of the game disappears. In each round of play, the responses given by each player will either be duplicates or not. Therefore, both players score together. The only way they can end up with different scores is if validity checking of answers is in place, and some answers are disqualified. In this simplified version of AI Categories, there is no validity checking, so both players will always score the same in a 2-handed game. If a model is playing against itself, this single score represents an individual score for that model, free of any reference to other models.
This is extraordinarily useful, because it means the scores obtained by this method can be compared to scores for any other model, as long as the prompts given were the same. For this stage of the test, I chose 4 of the 8 models which were tested in the 8-handed condition. I included a mix of models that showed qualitatively interesting results, high performance, and ready adaptation (Claude Sonnet and Haiku), those that showed interesting adaptations but poorer performance (Mistral 7B), and those that tended to be more rigid and lower performing (GPT-4o). API latency at the time of testing also played a part in removing DeepSeek from the test pool.
The Baseline Condition
An obvious issue here is that if model outputs are perfectly deterministic, or close to it, then in the simplest game condition (Blind Mode), where players are shown only identical prompts and no feedback from prior rounds or other players, we can expect them to output identical answers, and therefore all models would score zero.
In practice, this is not what happened with the models in this test (even with temperature set to 0.0 as with all tests in this series so far). Observing the scores under this baseline Blind condition therefore provides a useful estimate of the baseline entropy latent in the model’s output even when temperature is zero. It is helpful to know whether a model is fully deterministic at low temperature, in which case some variance in prompt input from player to player is necessary to “seed” entropy that can instigate divergence in the outputs of both models — even if it’s as subtle as where in the list of player responses one’s own response appears.
If the model contains an inherent stochastic component, even this addition of variability is unnecessary, and a small seed of entropy can be magnified with feedback to instigate wild model divergence even if inputs are identical. (We will see interesting examples of this phenomenon.)
Below are the scores from each model in a 2-handed self-play condition, with a possible maximum of 50 points.
Scores for all models were low, with only Sonnet managing to output more than 10 out of 50 responses. I suspect that Sonnet’s improved performance is largely due to its default step-by-step overt reasoning. An initial small seed of entropy can snowball over the course of Sonnet’s ruminations, resulting in meaningful model divergence between instances when time comes to choose an official response. The other models all mainly output just the response word or phrase itself, so the existing seed of randomness needs to be enough to shift the model output to a different attractor basin without the benefit of inference-time feedback loops, a much rarer occurrence.
In the next article in this series, we’ll see how the four models in this test managed to coordinate with their alter-egos to improve their scores in open information game conditions, their failure conditions, and what this shows us about model divergence and inference-time feedback-based learning.



